Research highlights
My research interests and expertise are in computational engineering and biomedical imaging. My work is uniquely informed by my transdisciplinary training and approaches, combining engineering, mathematical modeling, artificial intelligence (AI), and scientific computing. My ultimate goal is to exploit the power of computing to accelerate biomedical innovation and help resolve major challenges in medicine and public health, including early detection of cancers and improved treatment outcomes. My research focuses on developing novel computational, statistical, and AI approaches to 1) Advance emerging biomedical imaging modalities and address essential needs in clinical medicine and basic biomedical science; 2) Optimize the design of medical imaging instruments and improve diagnostic or screening performance; 3) Support informed clinical decision-making for patient-specific treatment regimes. I am playing a leading role in several projects using scientific computing and AI to unlock the full potential of quantitative biomedical imaging modalities, systematically assess imaging system design and image reconstruction methods by use of objective clinically relevant measurement of image quality and develop new computational approaches to estimate tumor perfusion from large-scale dynamic contrast-enhanced imaging data.
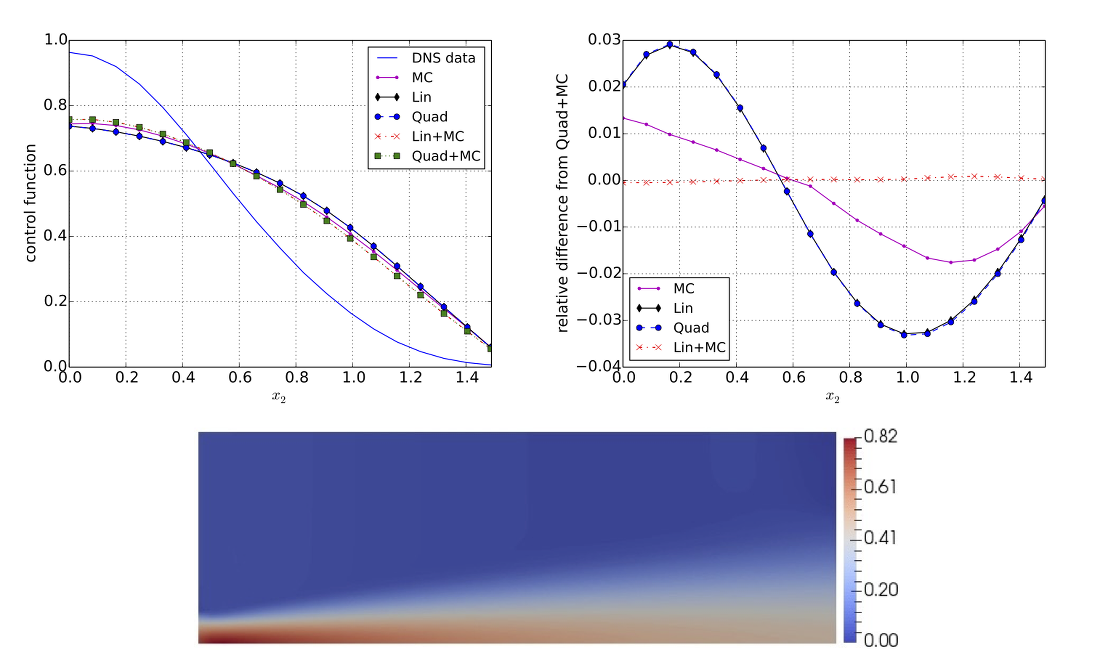
During my doctoral program and postdoctoral training, I made several important contributions to the field of computational science and engineering, and more specifically with regards to the use of large-scale numerical simulation as a tool to inform decision making under uncertainty. These included the use of patient-specific computational hemodynamics simulations to quantify wall shear stress and predict the risk of rupture of an aneurysm; the optimal control of the inlet condition of a turbulent jet to ensure proper mixing; and the use of information theoretic approaches (expected information gain) to optimally designing sensing systems.
As an Assistant Professor of Biomedical Engineering and core faculty of the Oden Institute, I am working on several projects aiming at advancing quantitative and functional image reconstruction algorithms with the ultimate goal of advancing the state-of-care for cancer diagnosis and treatment. In particular, my focus is on emerging acoustic and optical imaging modalities, such as photoacoustic computed tomography (PACT) and ultrasound computed tomography (USCT).
Find me on: Google Scholar.
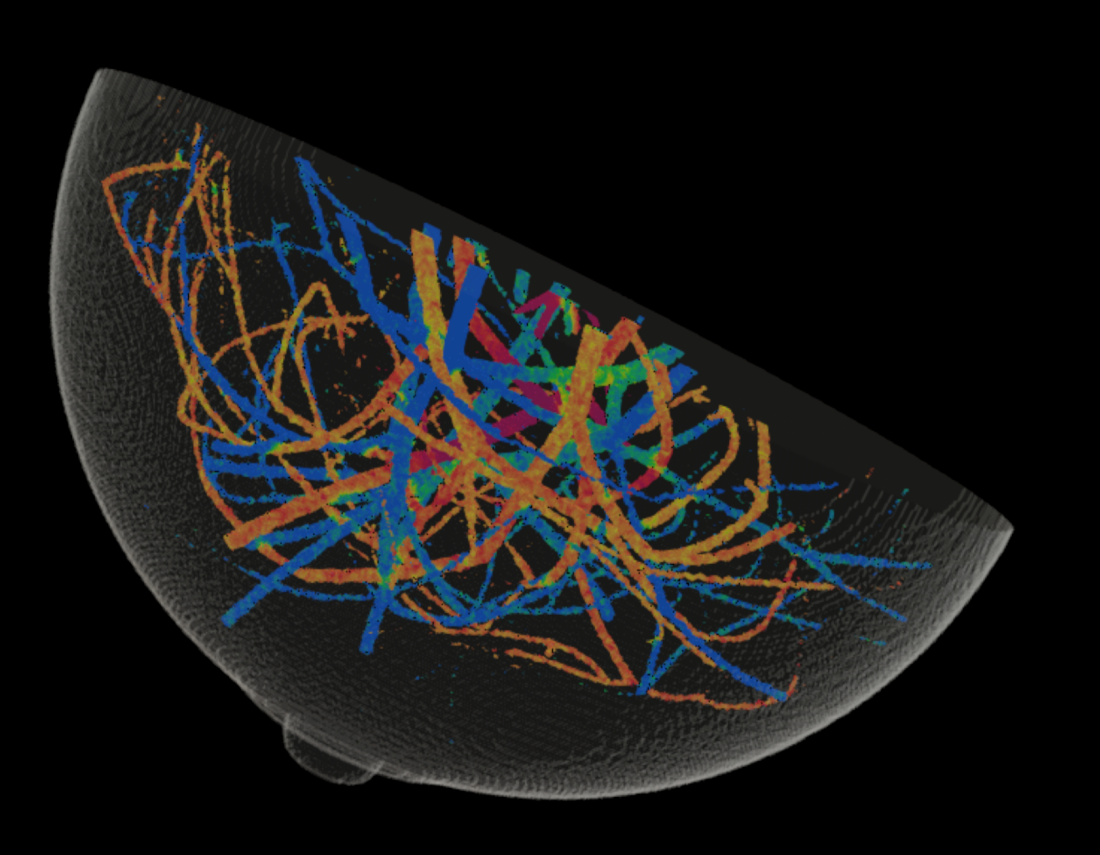 |
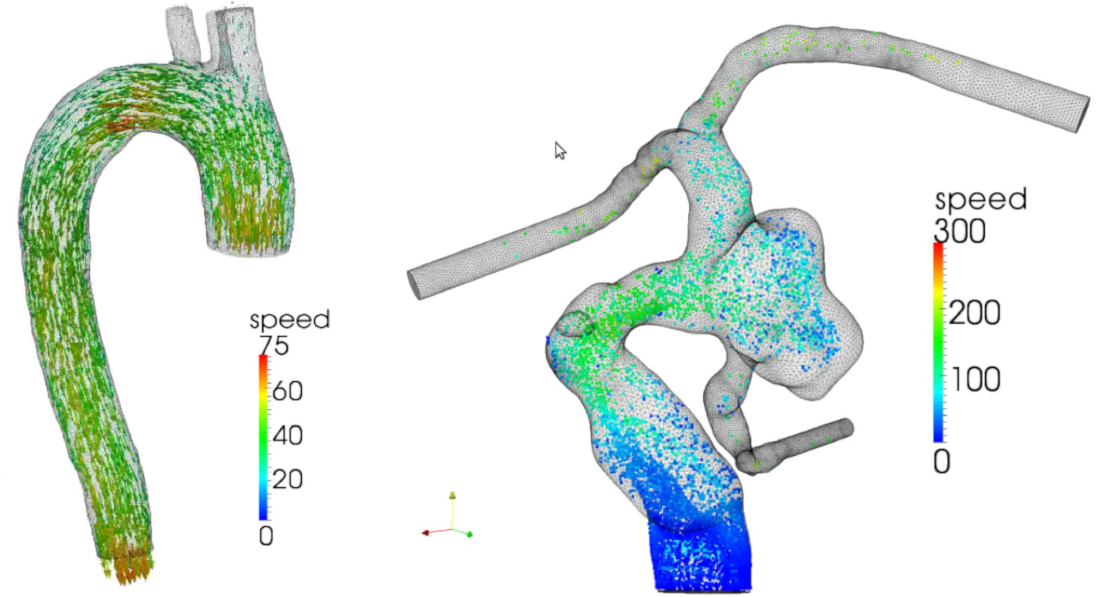 |
|---|---|
| Reconstruction algorithms for emerging medical imaging technologies (quantitative photoacoustic computed tomography) | Computational hemodynamics |
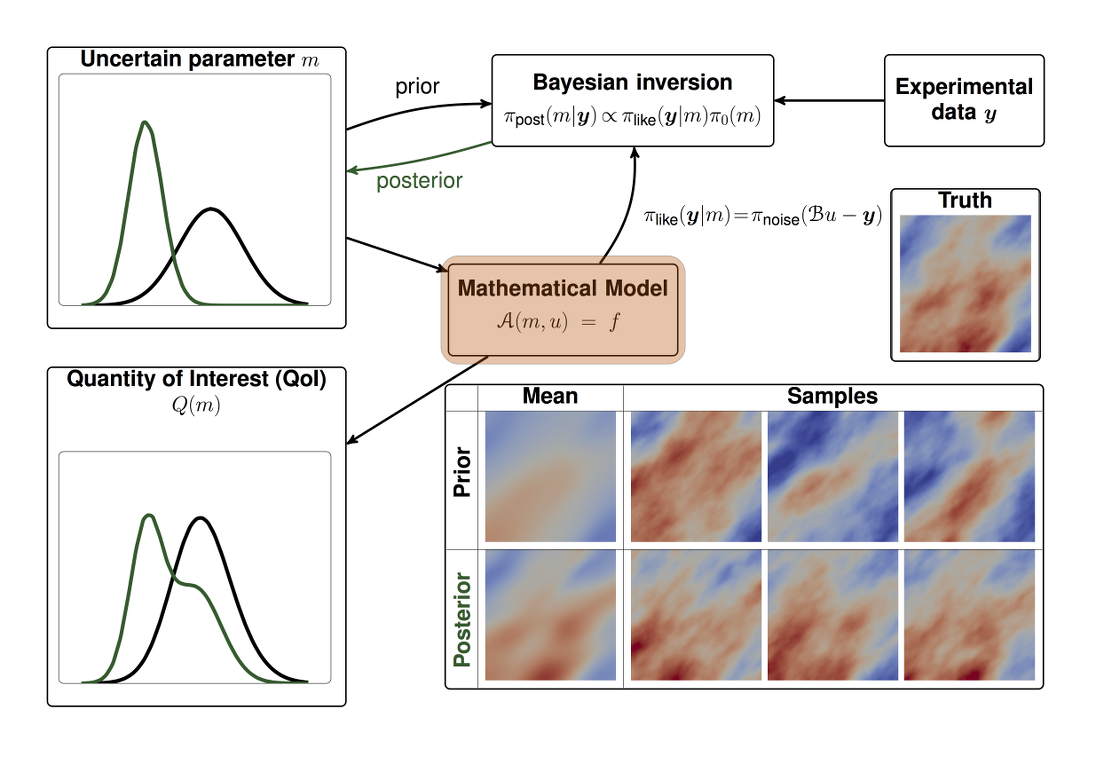 |
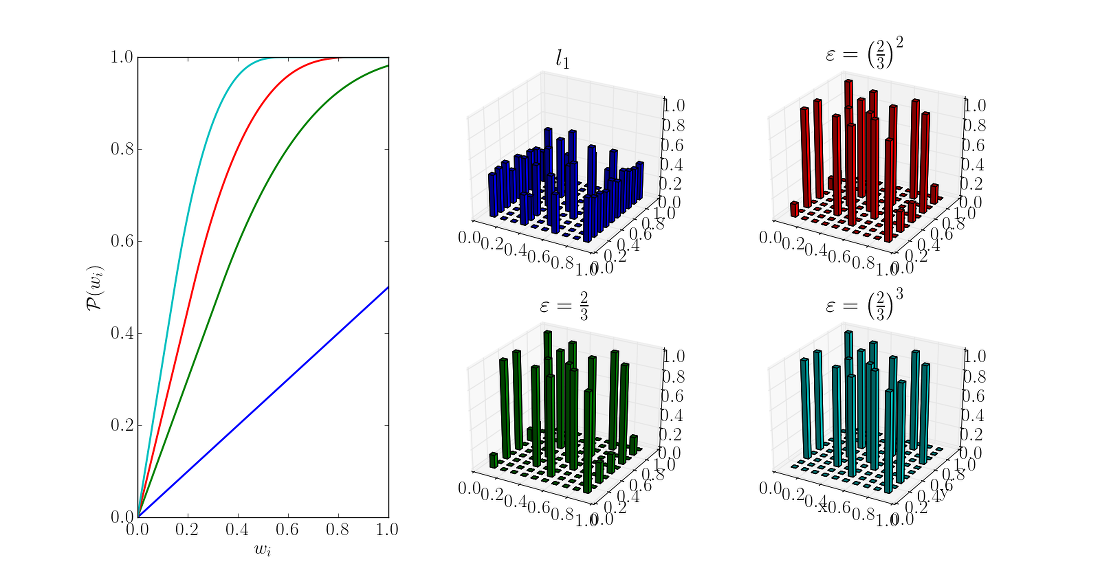 |
| The process of extracting knowledge from data by solving inverse problems | Bayesian optimal design of experiments with sparsifying penalty |
 |
 |
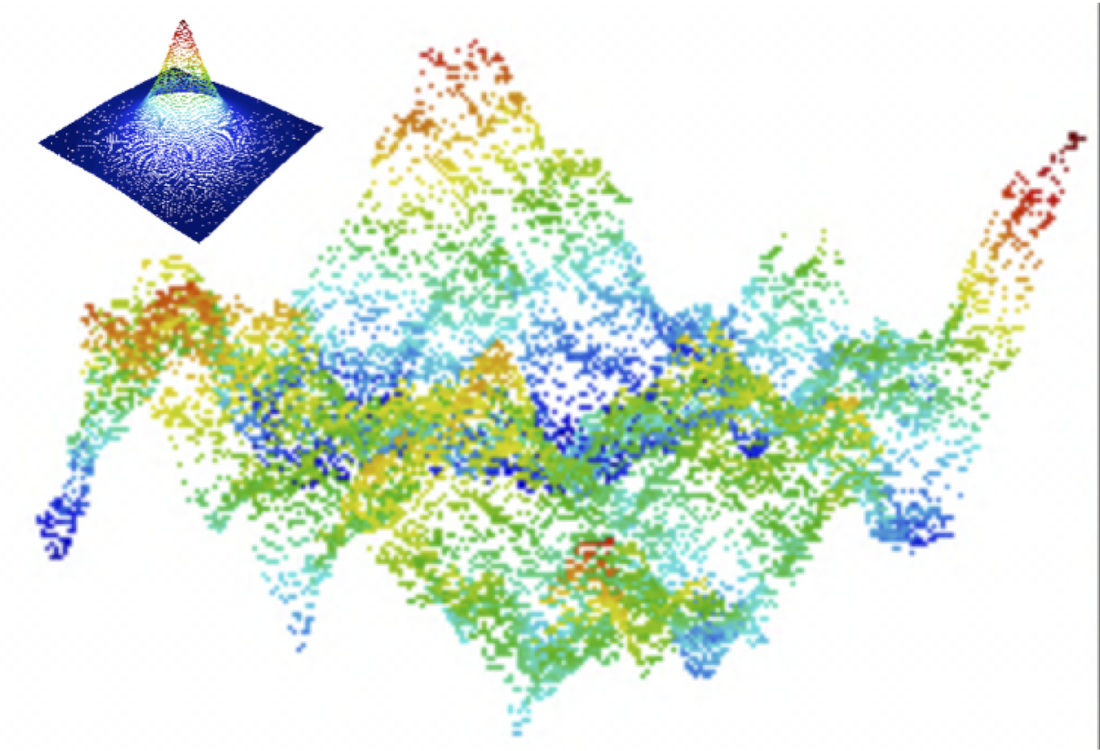
| Scalable sampling algorithms for Gaussian random fields | Optimization under uncertainty: application to turbulent jet |
 |
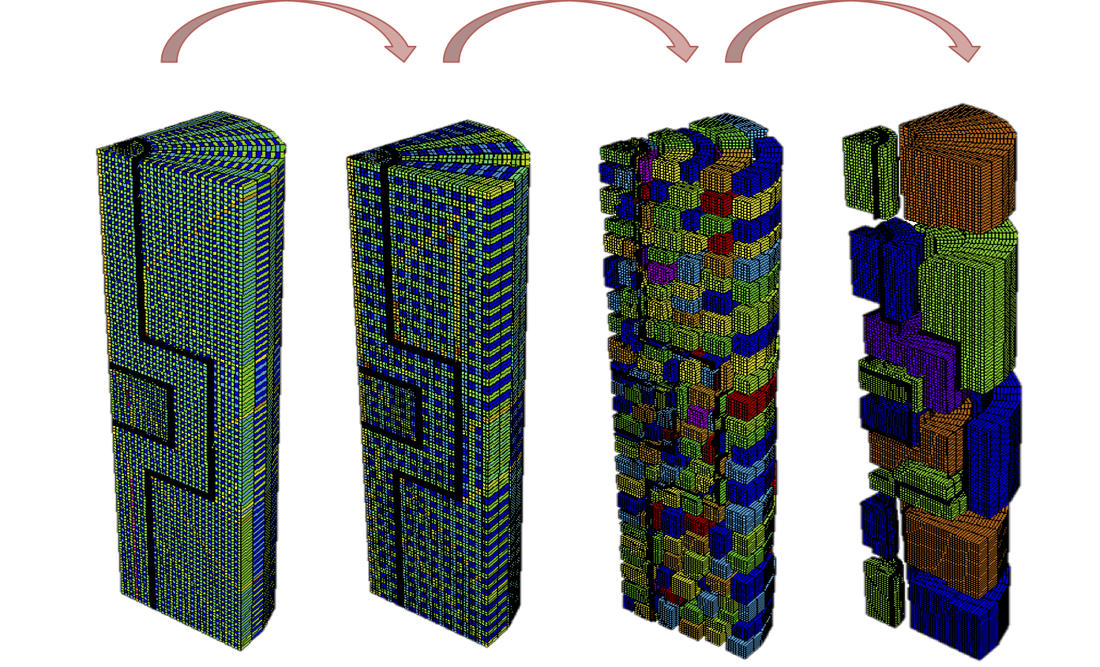 |
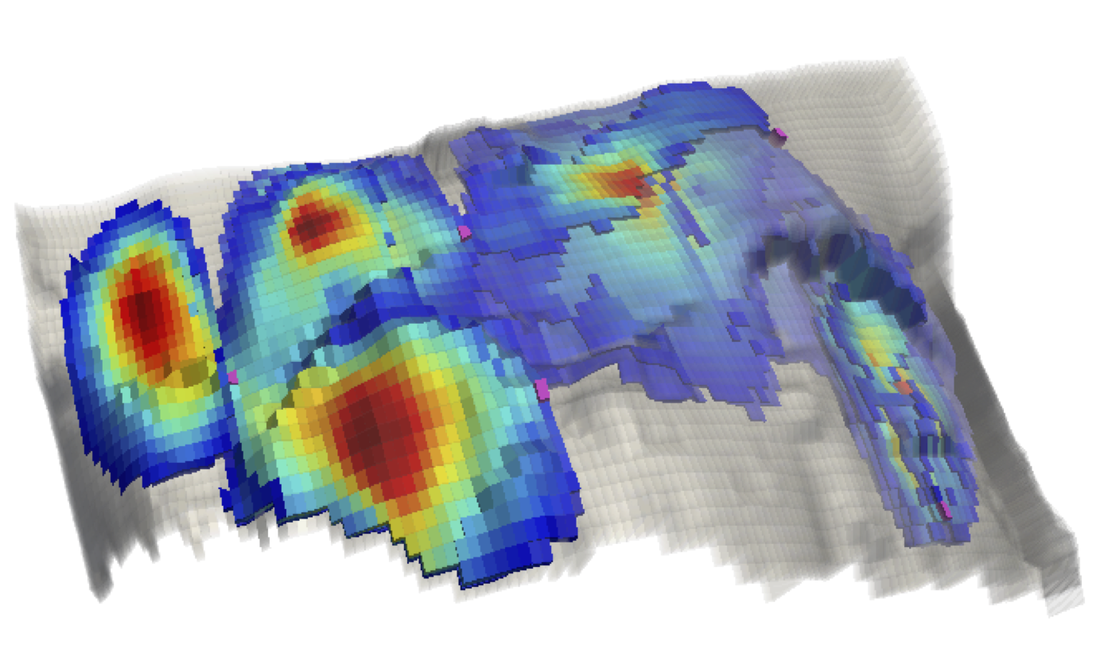
| Two-phases porous media flow | Hierarchy of agglomerated meshes for element-based AMG |